目标:
自行分析大部分数据结构和算法的时间、空间复杂度。在学习专栏中其他的时候,再不停地、有意识地去训练自己的复杂度分析能力。
掌握递推公式、递归树分析方法
重要程度:10
概念
复杂度也叫渐进复杂度,包括时间复杂度和空间复杂度,用来分析算法执行效率与数据规模之间的增长关系。
可以粗略地表示,越高阶复杂度的算法,执行效率越低。
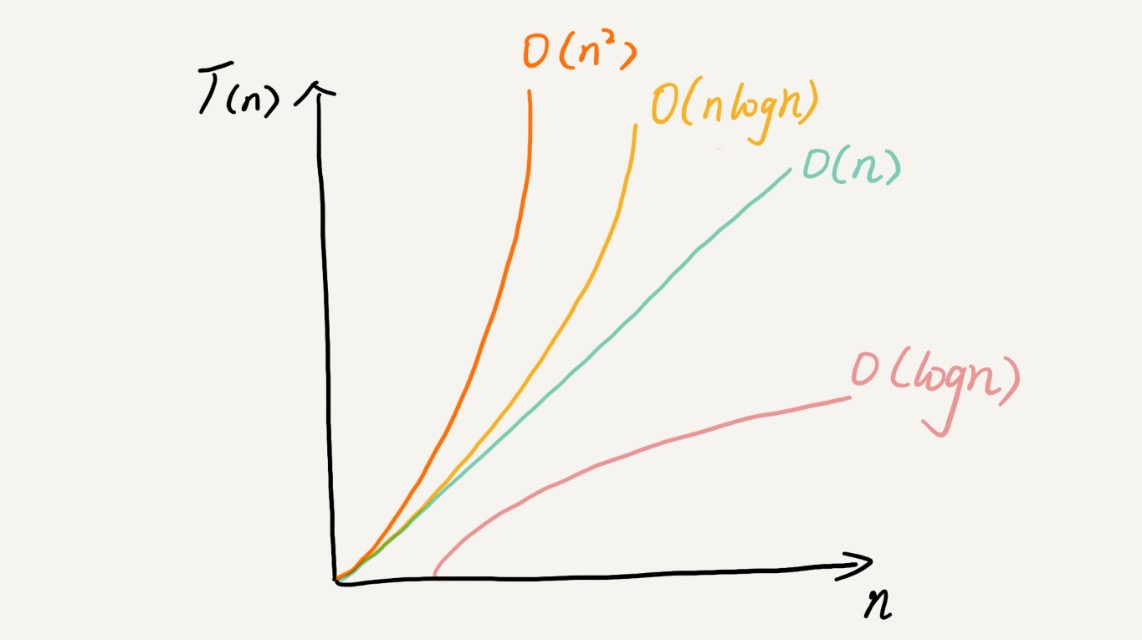
常见的复杂度从低阶到高阶有:O(1)、O(logn)、O(n)、O(nlogn)、O(n2)
时间复杂度
时间复杂度全称渐进时间复杂度(asymptotic time complexity),代码执行时间随数据规模增长的变化趋势。
大O时间复杂度表示法
T
T(n): 表示代码执行的时间
n: 表示数据规模的大小
f(n): 表示每行代码执行的次数总和。因为这是一个公式,所以用 f(n) 来表示
O: 表示代码的执行时间 T(n) 与 f(n) 表达式成正比
常见时间复杂度

时间复杂度分析方法
- 只关注循环执行次数最多的一段代码
- 加法法则:总复杂度等于量级最大的那段代码的复杂度
- 乘法法则:嵌套代码的复杂度等于嵌套内外代码复杂度的乘积
常见时间复杂度实例分析
O(1)
1 | int i = 8; |
O(logn)、O(nlogn)
1 | i=1; |
复杂度分析
最好、最坏情况时间复杂度
如下代码,最好为O(1),最坏为O(n)1
2
3
4
5
6
7
8
9
10
11
12// n表示数组array的长度
int find(int[] array, int n, int x) {
int i = 0;
int pos = -1;
for (; i < n; ++i) {
if (array[i] == x) {
pos = i;
break;
}
}
return pos;
}
平均情况时间复杂度
均摊时间复杂度
摊还分析法
空间复杂度
空间复杂度全称渐进空间复杂度(asymptotic space complexity),表示算法的存储空间与数据规模之间的增长关系。
常见的空间复杂度就是 O(1)、O(n)、O(n2),像 O(logn)、O(nlogn) 这样的对数阶复杂度平时都用不到。
复杂度与效率的关系